How much is a penalty really worth?

(Data from Opta.)

Conventional Wisdom

The public analytics community as a whole assign a value of 0.76 XG (XG explained) to a penalty. Is this correct?
(Disclaimer: I will not be going into the issue of whether or not penalties should be included in single game summaries or timelines)

Origin

With a large dataset it is easy to calculate a quick estimate for the probability of a penalty resulting in a goal. Looking at the outcome of penalties awarded below, excluding penalty shootouts (they’re converted at a different rate), we can see where the widely used figure of 0.76 comes from.

Type	Total	%
Goal	6340	0.7596
Saved	1492	0.1788
Missed	289	0.0346
Post	225	0.0270

Improvement

I was watching a game recently and this happened. How often do these kind of chances arise, and how likely are they to result in goals?

<iframe width="560" height="315" src="https://www.youtube.com/embed/QLkQ_SdO0a8?rel=0&showinfo=0" frameborder="0" allow="autoplay; encrypted-media">

Penalty Rebounds

Definition

I denote a shot to be a penalty rebound if:

The shot occurs directly after a penalty that is either saved or hits the post. It is the first action taken by the same team after the penalty (i.e no passes made).

I also chose to log the time between the taking of the penalty and the penalty rebound for sanity checking purposes.

Validation

Click for larger graphs.

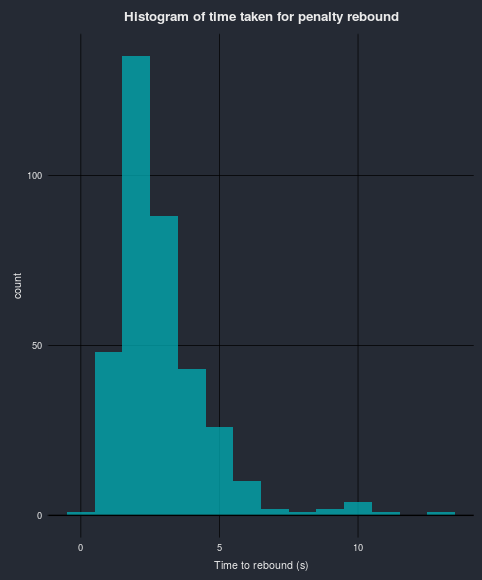
There is a total of 368 “penalty rebounds” in my dataset. Looking at the histogram above, the majority of the “time_to_rebound’s” fall within a reasonable bound, there are a few entries > 10 seconds that look suspicious. Looking at one of the entries with a large time_to_rebound (11 seconds), a penalty rebound does occur and the actual “time_to_rebound” is less than the 11 seconds.

<iframe width="560" height="315" src="https://www.youtube.com/embed/8D4ZklbHLrw?rel=0&showinfo=0&start=57" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen>

The locations of the rebounds intuitively make sense too, however there are a few points around the x=70 position that look questionable. Once again looking at a rebound with one of the most extreme x co-ordinates (x=71, y=58), we can be confident that this fits the description of a penalty rebound.

<iframe width="560" height="315" src="https://www.youtube.com/embed/bQ_RyKO6XIw?rel=0&showinfo=0&start=27" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen>

Summary Statistics

Looking at the whole set of penalty rebounds gives the summary statistics below.

#	Mean XG/shot	Mean Goals/shot	Mean error	Mean absolute error	RMSE
368	0.33	0.42	0.089	0.35	0.42

(Mean absolute error & RMSE explained)
I was surprised by the errors between the model predictions and the actual outcome of the penalty rebounds. I was expecting them to be much greater, due to:

• Keeper being grounded, or very recently grounded.
• Much less likely for defenders to be in-between the shooter & the goal than any other normal shot.

Improvement

I re-trained the XG model using penalty rebound as a feature (368 shots out of a total of over 70,000 shots). The newly trained model predicted a mean XG per shot of 0.38 for the penalty rebounds, and had a minuscule improvement over the old model in terms of its RMSE for both the penalty rebound shots, and also all shots. Summary statistics for the new model are shown below.

#	Mean XG/shot	Mean Goals/shot	Mean error	Mean absolute error	RMSE
368	0.38	0.42	0.037	0.35	0.41

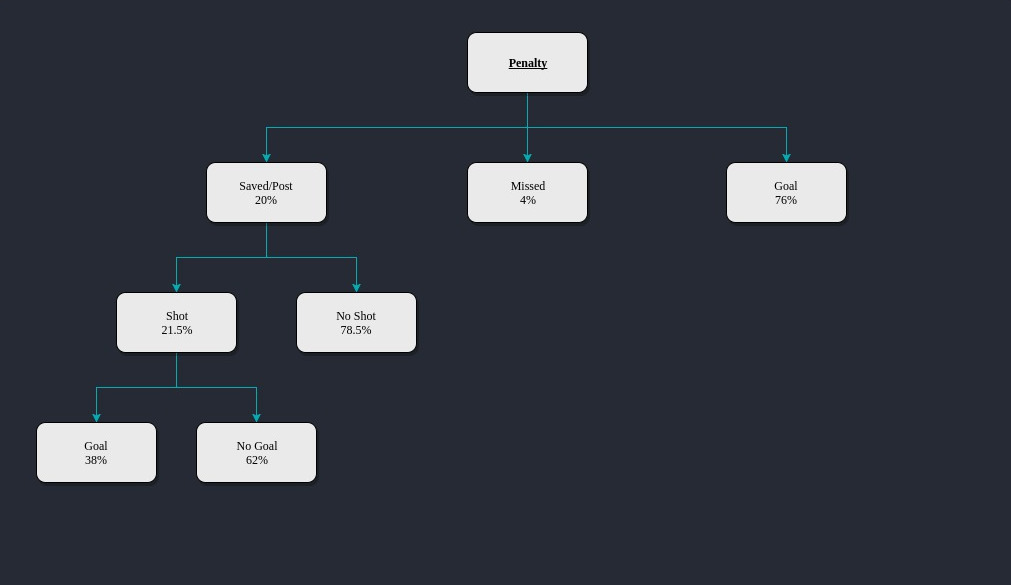
Following the tree above, and using the XG model value of 0.38 for a penalty rebound, a penalty results in a goal in 78% of occurrences.

0.76 + (0.2 x 0.215 x 0.38) = 77.6%

Note

Using 0.78 as the estimated value for a penalty awarded only makes sense if any shots that would be classified as a penalty rebound are removed too.